Information divergences

Minimum Distance/Divergence Methods

Our research includes statistical estimators of probability densities within minimum distance principle based on the theory of disparities or information divergences such as Kolmogorov and Lévy distances, discrepancy, Cramer-von Mises distance, phi-divergences, subdivergences, Rényi decomposable measures, etc. The minimum distance estimators (MDE) are increasingly being used when the classical maximum likelihood theory breaks down due to unbounded likelihood problems such as mixtures of continuous distributions, heavy tailed distributions with unknown location and scale parameters, or distributions with a parameter dependent support.

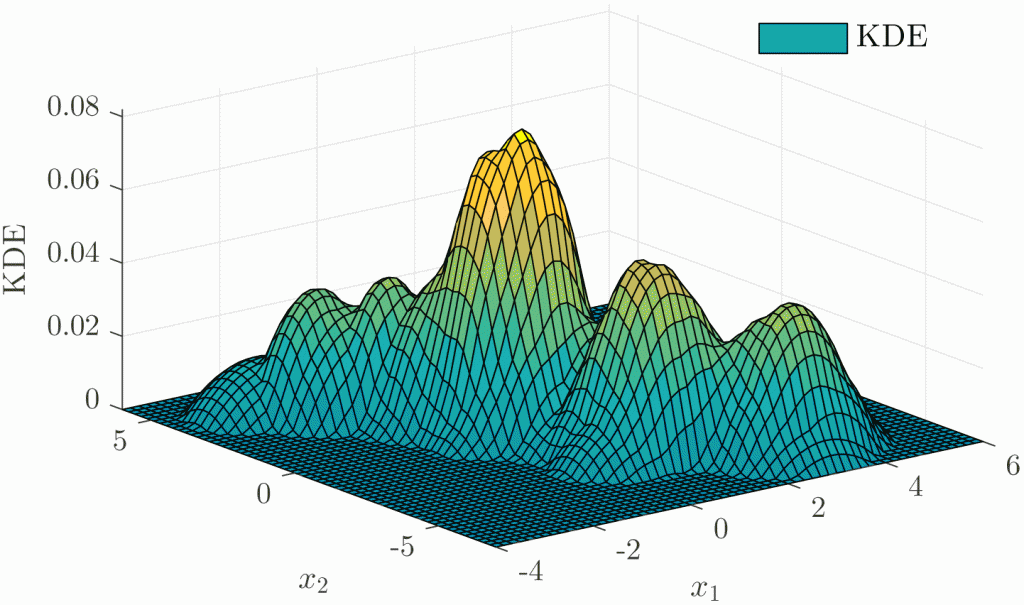
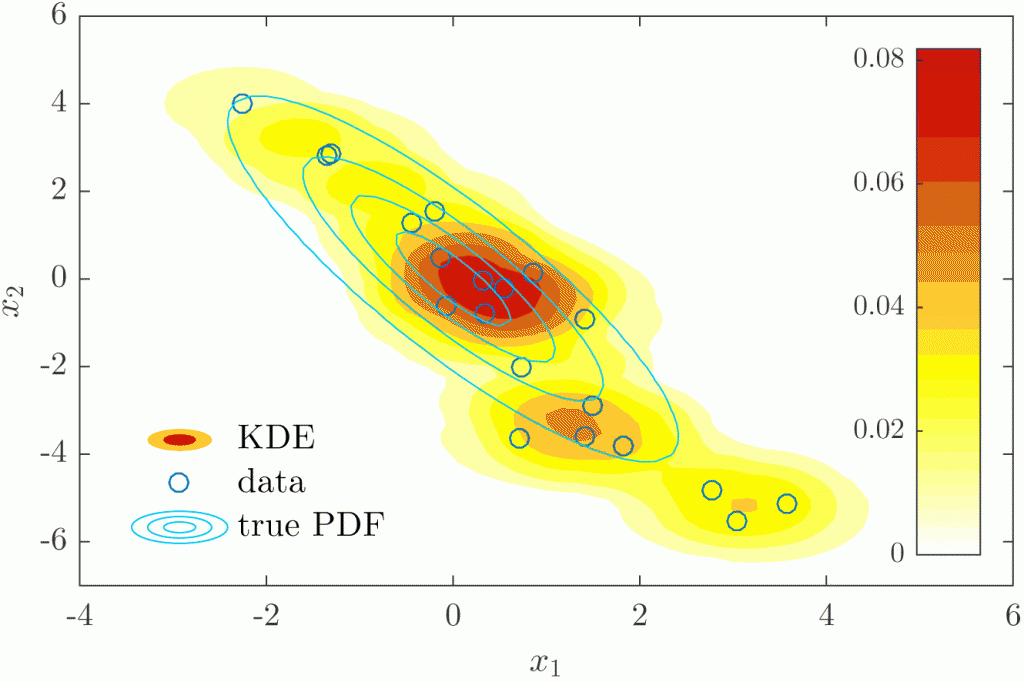
We deal with sufficient conditions for the existence of the approximate minimum distance estimators (AMDE) and also, in this context, with computer simulations to evaluate and verify the main statistical properties of these estimates, mainly their consistency, robustness, and efficiency. For example, our simulation experiments empirically study performance of the approximate minimum Kolmogorov estimator (AMKE) and some histogram and KDE kernel -based variants of approximate minimum divergence estimators, like power type and LeCam, under various distributions. The simulations analyses the potential of model discrimination through different families of distributions.

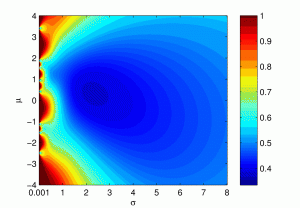
In real applications, data are rarely uncontaminated. Hypothesis testing on contaminated data is therefore and urgent matter. We process the robust Wald-type parametric tests based on minimum Renyi distance estimator both for generated and real data samples. Again, we carry out simulations for all selected families of distributions and comment on the optimal choice of the tuning parameters. In addition, we compare our test with other widely used statistical tests.

Finally, all these MDE concepts are then used in structural material defectoscopy as in architecture for projection of earthquake energy dissipating dampers, ultrasonic signal processing, acoustic emission source characterization in energetics or aircraft industry, moreover in high energy physics, e.g. in neutrino tracking and 3D prong reconstruction based on statistical hypotheses testing of the corresponding neutrino energy probability distribution (NOvA/DUNE Fermilab).

Cooperation

Prof. Domingo Morales (CIO UMH Elche ES): cooperation on divergence methods in statistics
Ing. Miroslav Kárný, DrSc. (Department of Adaptive Systems, ÚTIA AV ČR): cooperation on divergence methods in decision making
Ing. Jitka Hrabáková (FIT ČVUT v Praze): cooperation on minimum Kolmogorov/Cramér density estimation

Members

Václav Kůs

assistant professor at FNSPE CTU in Prague

(robustness, consistency, and efficiency of minimum distance/divergence estimators)

Zuzana Dvořáková

Ph.D. student at FNSPE CTU in Prague

(distance/divergence based classiﬁcation of stochastic signals – acoustic emission)

Jitka Hrabáková

Ph.D. student at FNSPE CTU in Prague

(consistency and robustness of minimum distance estimators with simulation results)

Kristina Jarůšková

Ph.D. student at FNSPE CTU in Prague (full-time CERN)

(statistical separations and machine learning methods/software for big data)

Graduates

Iva Frýdlová (Mittaschová)

(performances of modified power divergence estimators in the normal models: simulation and comparative Study)

Petr Bouř

(development of statistical nonparametric and divergence methods for data processing in NOvA experiments)

Richard Finger

(asymptotic properties and robustness of minimum score/pseudo-distance statistical tests)

Jan Kučera

(Rényi divergence estimators of probability densities – robustness and efficiency testing)

Jitka Hrabáková (Hanousková)

(minimum Kolmogorov-Cramér distance density estimators)

Radim Demut

(robust properties of minimum divergence density estimators)

Ondřej Fránek

(computer simulation on minimum Kolmogorov distance density estimators)

Lucie Hanáková

(robust divergence statistic techniques for signal separation from decay processes at Fermilab)

Michaela Sluková

(statistical analysis and data classification using the methods based on phi-divergences)

Kateřina Hladká

(divergence based separation of probability distributions derived from particle physic experiments )

Significant papers

Kůs, V., Finger, R., Unifying approach to score based statistical inference in physical sciences, Journal of Physics: Conf. Ser., 2019, 1391 (012124), ISSN 1742-6588. DOI: 10.1088/1742-6596/1391/1/012124.
Kůs, V., Jarůšková K., Divergence decision tree classification with Kolmogorov kernel smoothing in high energy physics, Journal of Physics: Conf. Ser., 2021,1730 (012060), ISSN 1742-6588. DOI: 10.1088/1742-6596/1730/1/012060.
Kůs, V., Kučera, J. and Morales, D., Numerical enhancements for robust Rényi decomposable minimum distance estimators. Journal of Physics: Conference Series, 2018, 1141 1-5. ISSN 1742-6588. DOI 10.1088/1742-6596/1141/1/012037.
Kůs, V., Morales, D., Hrabáková, J., Frýdlová, I., Existence, Consistency and Computer Simulation for Selected Variants of Minimum Distance Estimators. Kybernetika, 2018, 54(2), 336-350. ISSN 0023-5954. DOI 10.14736/kyb-2018-2-0336.
Hrabáková, J., Kůs, V., Notes on consistency of some minimum distance estimators with simulation results. Metrika. 2017, 80(2), 243-257. ISSN 0026-1335. DOI 10.1007/s00184-016-0601-0.
Kožená, C., Kůs, V., Dos Santos, S., Hysteresis and memory effects in skin aging using PM space density identification. Biennial Baltic Electronics Conference (BEC), USA: IEEE Computer Society, 2016, p.179-182. ISSN 1736-3705, ISBN 978-1-5090-1393-7. DOI 10.1109/BEC.2016.7743758
Hrabáková, J., Kůs, V., The Consistency and Robustness of Modified Cramer-Von Mises and Kolmogorov-Cramer Estimators. Communication in Statistics-Theory and Method, 2013, 42(20), 3665-3677. ISSN 0361-0926. DOI 10.1080/03610926.2013.802806.
Frýdlová, I., Vajda, I., Kůs, V., Modified Power Divergence Estimators in Normal Model- Simulation and Comparative Study. Kybernetika. 2012, 48(4), 795-808. ISSN 0023-5954, WOS: 000310190200009,